Roulette Physics Formula

Jun 07, 2016 According to Muller, a colleague came up with the method of beating the roulette table, based on physics, which exploits the 'bet in play' rule which encourages people to gamble. We first use the probability density formula, if the result for F fails, we move onto the cumulative distribution function. Only time F Fails if it is larger than 36. A ALWAYS corresponds to the latest spin. We simply plug these variables into the probability density formula: 36 x ( 26 + 1 )-( 2 + 1 ) Always place a 1 in the formula instead.
Roulette is a game of numbers and chance. You can sit around studying the odds in roulette and the outcomes of trying to predict where that little ball will next end up but unfortunately you will be wasting a great deal of your time. Roulette is a game to be enjoyed. Sometimes you’ll win and sometimes you’ll lose. It’s a game that has been played for centuries and no-one yet has found a way to truly beat the game. The game has been used to help develop statistical theories and processes such as Karl Pearson´s Goodness of Fit test. Could maths return the favour and help crack the code?
Countless people through the ages have tried to crack the roulette code using mathematics. Some of the more famous roulette systems are beased on mathematical sequences, strategies like the Fibonacci System, for example.
Mathematics seems the most obvious way in which you can attempt to beat the dealer but predicting any result is simply a matter of probability. The entire game is based upon independent events, which therefore means that any event that occurs when the wheel spins and the ball lands has no affect or influence on any previous or future spin. You should also check out our page that covers physics in roulette, by the way.
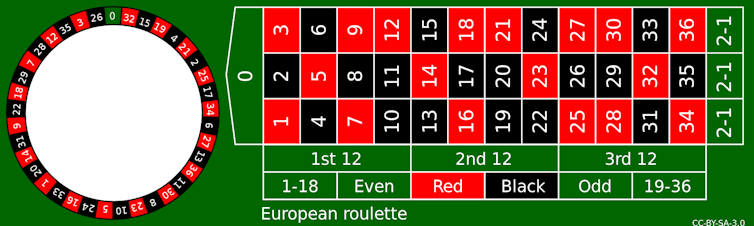
In European Roulette the payout on hitting any one of the 36 red or black numbers on the wheel is 35 to 1. It’s the highest payout you can achieve with a single bet and so of course means that the probability is the lowest (at just 2.7% in fact). For an averagely better chance of winning many players will simply place an even-money bet on something like red or black, odds or evens or any one of the numbered groups. The probability is a massive 48.6% but the payout is just 1:1. But if the bet is pretty much a 50-50 chance then why is it only 48.6% and not 50%? Well, don’t forget that the European table also includes the green zero pocket so this does mean that the odds will be slightly lower than 50/50. In fact, this little zero pocket is what gives the casino its roulette house edge, when combined with the payout structure.
British engineer Joseph Jagger did manage to use mathematics and predictability when he managed to win a significant sum of money on his visit to Monte Carlo in 1875. Jagger has hired 6 clerks to visit the casino Beaux-Arts Casino in Monaco to record all the outcomes of 6 different roulette wheels over a period of time. Using these findings he was able to discover a pattern of a group of numbers that kept coming in more frequently than others on just one of these wheels. He ended up placing his bets on this particular wheel using these numbers in question and was able to accumulate hundreds and thousands of pounds of winnings.
However, Jagger hadn’t uncovered an incredible flaw in the game itself. He had simply exposed the fact a roulette wheel in the world’s biggest gambling capital merely had a mechanical imbalance which gave the wheel a clear bias towards certain outcomes. And the problem with that discovery, was that the casino discovered it as well. And they fixed the wheel!
Is it possible to win at the roulette tables? There are people who have actually, provably managed to do so. Despite many proposed “systems” there are only two profitable ways to play roulette. One can either exploit an unbalanced wheel, or one can exploit the inherently deterministic nature of the spin of both ball and wheel. Casinos will do their utmost to avoid the first type of exploit. The second exploit is possible because placing wagers on the outcome is traditionally permitted until some time after the ball and wheel are in motion. That is, one has an opportunity to observe the motion of both the ball and the wheel before placing a wager.
Taking advantage of biased wheels

Unbalanced wheel
The archetypal tale of the first type of exploit is that of a man by the name of Jagger (various sources refer to him as either William Jaggers or Joseph Jagger, or some permutation of these). Jagger, an English mechanic and amateur mathematician, observed that slight mechanical imperfection in a roulette wheel could afford sufficient edge to provide for profitable play. According to one incarnation of the tale, in 1873 he embarked for the casino of Monte Carlo with six hired assistants. Once there, he carefully logged the outcome of each spin of each of six roulette tables over a period of five weeks. Analysis of the data revealed that for each wheel there was a unique but systematic bias. Exploiting these weaknesses he gambled profitably for a week before the casino management shuffled the wheels between tables. This bought his winning streak to a sudden halt. However, he soon noted various distinguishing features of the individual wheels and was able to follow them between tables, again winning consistently. Eventually the casino resorted to re- distributing the individual partitions between pockets. A popular account, published in 1925, claims he eventually came away with winnings of £65,0008. The success of this endeavor is one possible inspiration for the musical hall song “The Man Who Broke the Bank at Monte Carlo” although this is strongly disputed.
Statistical analysis
Similar feats have been repeated elsewhere. The noted statistician Karl Pearson provided a statistical analysis of roulette data, and found it to exhibit substantial systematic bias. However, it appears that his analysis was based on flawed data from unscrupulous scribes (apparently he had hired rather lazy journalists to collect the data).
Irregularities
In 1947 irregularities were found, and exploited, by two students, Albert Hibbs and Roy Walford, from Chicago University. Following this line of attack, S.N. Ethier provides a statistical framework by which one can test for irregularities in the observed outcome of a roulette wheel. A similar weakness had also been reported in Time magazine in 12 February 1951. In this case, the report described various syndicates of gamblers exploiting determinism in the roulette wheel in the Argentinean casino Mar del Plata during 1948. The participants were colorfully described as a Nazi sailor and various “fruit hucksters, waiters and farmers”.
Using physics and computers
Henri Poincaré
The second type of exploit is more physical (that is, deterministic) than purely statistical and has consequently attracted the attention of several mathematicians, physicists and engineers. One of the first was Henri Poincaré in his seminal work Science and Method. While ruminating on the nature of chance, and that a small change in initial condition can lead to a large change in effect, Poincaré illustrated his thinking with the example of a roulette wheel (albeit a slightly different design from the modern version).
He observed that a tiny change in initial velocity would change the final resting place of the wheel (in his model there was no ball) such that the wager on an either black or red (as in a modern wheel, the black and red pockets alternate) would correspondingly win or lose. He concluded by arguing that this determinism was not important in the game of roulette as the variation in initial force was tiny, and for any continuous distribution of initial velocities, the result would be the same: effectively random, with equal probability. He was not concerned with the individual pockets, and he further assumed that the variation in initial velocity required to predict the outcome would be immeasurable. It is while describing the game of roulette that Poincaré introduces the concept of sensitivity to initial conditions, which is now a cornerstone of modern chaos theory.
The first roulette computer
A general procedure for predicting the outcome of a roulette spin, and an assessment of its utility was described by Edward Thorp in a 1969 publication for the Review of the International Statistical Institute. In that paper, Thorp describes the two basic methods of prediction. He observes (as others have done later) that by minimizing systematic bias in the wheel, the casinos achieve a mechanical perfection that can then be exploited using deterministic prediction schemes.
He describes two deterministic prediction schemes (or rather two variants on the same scheme). If the roulette wheel is not perfectly level (a tilt of 0.2◦ was apparently sufficient — we verified that this is indeed more than sufficient) then there effectively is a large region of the frame from which the ball will not fall onto the spinning wheel. By studying Las Vegas wheels he observes this condition is meet in approximately one third of wheels. He claims that in such cases it is possible to garner a expectation of +15%, which increased to +44% with the aid of a ‘pocket-sized’ computer. Some time later, Thorp revealed that his collaborator in this endeavor was Claude Shannon17, the founding father of information theory.
| Math professor Ed. Thorp |
Richard A. Epstein
In his 1967 book the mathematician Richard A. Epstein describes his earlier (undated) experiments with a private roulette wheel. By measuring the angular velocity of the ball relative to the wheel he was able to predict correctly the half of the wheel into which the ball would fall. Importantly, he noted that the initial velocity (momentum) of the ball was not critical. Moreover, the problem is simply one of predicting when the ball will leave the outer (fixed rim) as this will always occur at a fixed velocity. However, a lack of sufficient computing resources meant that his experiments were not done in real time, and certainly not attempted within a casino.
The Eudaemons
Subsequent to, and inspired by, the work of Thorp and Shannon, another widely described attempt to beat the casinos of Las Vegas was made in 1977-1978 by Doyne Farmer, Norman Packard and colleagues, who’s team was called “The Eudaemons“. It is supposed that Thorp’s 1969 paper had let the cat out of the bag regarding profitable betting on roulette. However, despite the assertions of Bass, Thorp’s paper is not mathematically detailed (there is in fact no equations given in the description of roulette). Thorp is sufficiently detailed to leave the reader in no doubt that the scheme could work, but also vague enough so that one could not replicate his effort without considerable knowledge and skill.
Farmer, Packard and colleagues implemented the system on a 6502 microprocessor hidden in a shoe and proceeded to apply their method to the various casinos of the Las Vegas Strip. The exploits of this group are described in detail in Bass. The same group of physicists went on to apply their skills to the study of chaotic dynamical systems and also for profitable trading on the financial markets. In Farmer and Sidorowich’s landmark paper on predicting chaotic time series the authors attribute the inspiration for that work to their earlier efforts to beat the game of roulette.
The Ritz casino attack
Less exalted individuals have also been employing similar schemes, in some cases fairly recently. In 2004, the BBC carried the report of three gamblers (described only as “a Hungarian woman and two Serbian men”) arrested by police after winning £1,300,000 at the Ritz Casino in London. The trio had apparently been using a laser scanner and their mobile phones to predict the likely resting place of the ball. Happily, for the trio but not the casino, they were judged to have broken no laws and allowed to keep their winnings.
The physics approach
In their 2012 paper, Predicting the outcome of roulette, Michael Small and Chi Kong TseThe come to these conclusions:
First, deterministic predictions of the outcome of a game of roulette can be made, and can probably be done in situ. Hence, the tales of various exploits in this arena are likely to be based on fact.
Roulette Physics Formula
Second, the margin for profit is quite slim. Minor manipulation with the frictional resistance or level of the wheel and/or the manner in which the croupier actually plays the ball (the force with which the ball is rolled and the effect, for example, of axial spin of the ball) have not been explored here and would likely affect the results significantly.
Roulette Physics Formula Physics
Hence, for the casino the news is mostly good. Minor adjustments will ameliorate the advantage of the physicist-gambler. For the gambler, one can rest assured that the game is on some level predictable and therefore inherently honest.